The DGAs of Necurs
- The First DGA
- Connectivity Checks
- DGA Caller
- The Heart of the First DGA
- Pseudorandom Number Generator
- Comparison with Facebook's or Microsoft's IP
- Summary
- The Second DGA
- The Third DGA
- Sequence Numbers
- DGA Caller
- The DGA
- Summary
The DGA in this blog post has been implemented by the DGArchive project.
For more information about the malware in this blog post see the Malpedia entry on Necurs.
Necurs is a malware that opens a backdoor on infected systems, see NECURS: The Malware That Breaks Your Security. A broad analysis of the malware can be found in the three part series The Curse of Necurs by Peter Ferrie.
This post focuses exclusively on the network traffic of Necurs, in particular the used domains. Necurs features three different sets of hostnames that serve different purposes. Although all three sets reek of domain generation algorithm (DGA), only the first and last set are actually generated algorithmically. The following example traffic shows the different stages of the callback attempts with number 3, 4 and 6 marking the three malicious domains batches:
1.---- 13:09:39.635819000 facebook.com
+- 13:09:39.638039000 0.pool.ntp.org
2.--| 13:09:39.998526000 1.pool.ntp.org
+- 13:09:40.020627000 2.pool.ntp.org
+- 13:09:40.027471000 sxotmrxwhddr.com
| 13:09:40.028494000 btysiiquuc.com
3.--| 13:09:40.032591000 kfncxvayakmb.com
+- 13:09:40.033539000 vmslcvvocseu.com
+- 13:09:40.688199000 qcmbartuop.bit
| 13:09:41.699491000 qcmbartuop.bit
4.--| 13:09:42.716128000 qcmbartuop.bit
| (... 16 times total)
+- 13:16:32.364351000 qcmbartuop.bit
5.---- 13:16:49.187559000 facebook.com
+- 13:16:49.516477000 boymlujtgp.nu
| 13:16:49.520651000 ybynentfsjvmsgtktcoog.im
| 13:16:49.527701000 oiijxplrnmvgskxwaye.ru
6.--| 13:16:49.529669000 imgirmyddbsniuh.pw
| 13:16:49.834913000 ultrttvbvjaanrj.jp
| (... 2048 total)
+- 13:18:03.607552000 porgtemsbycy.ki
The following list gives a brief summary of the source and purpose of the domains. See the respective section for an in-depth analysis of the three DGA sets.
- Necurs starts by checking internet connectivity by resolving facebook.com or microsoft.com.
- The malware then contacts three NTP pools to get the accurate date and time.
- Next, four DGA domains are generated by the first dga with top level domain .com. The domains are unpredictable and can therefore not be sinkholed or used to identify Necurs samples when taken in isolation. The purpose of the domains is to detect simulated internet in lab environments
- If the lab detection test passes, Necurs will try sixteen domains from a hard-coded list of pseudo-DGA domains, see second dga. Necurs will reuse domains if the list contains less than 16 domains. The analysed sample, for example, only has one hard-coded domain which will therefore be repeated 16 times. Necurs sleeps between 1 and 20 seconds after each failed connection attempt, which mounts up to about 5 minutes before the malware moves on to the next stage. The hard-coded domains are probably the main C&C domains.
- Another connectivity check to facebook.com or microsoft.com is made before Necurs resorts to the last DGA.
- The third dga finally checks up to 2048 different domains. One special feature is the large list of 43 different top level domains, some of which are quite exotic. The DGA is time-dependent — the domains change every four days. The DGA is probably a backup in case the set of hard-coded domains no longer work.
The First DGA
Connectivity Checks
Necurs makes a connectivity check to either facebook.com or microsoft.com before the first set of DGA domains are tested:
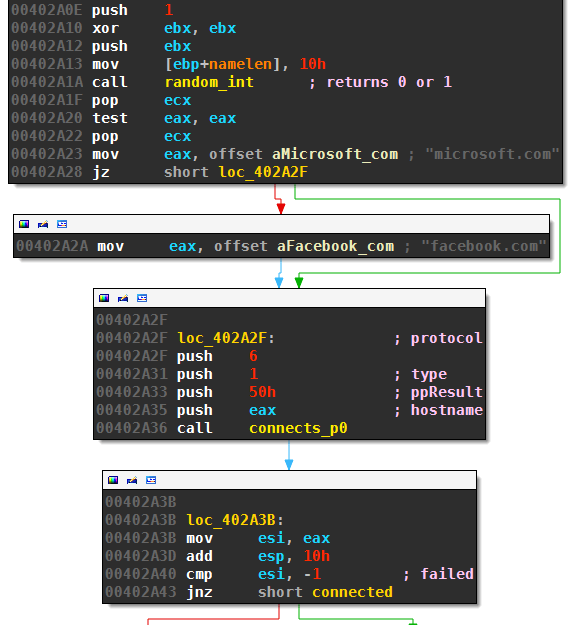
The routine random_int(0,1) returns 0 or 1 (the implementation of random_int is discussed below). The malware aborts the callback attempt if it can’t resolve and contact the domain of Facebook or Microsoft as the case may be.
DGA Caller
Necurs then launches four threads that attempt to resolve domains generated by the first DGA:
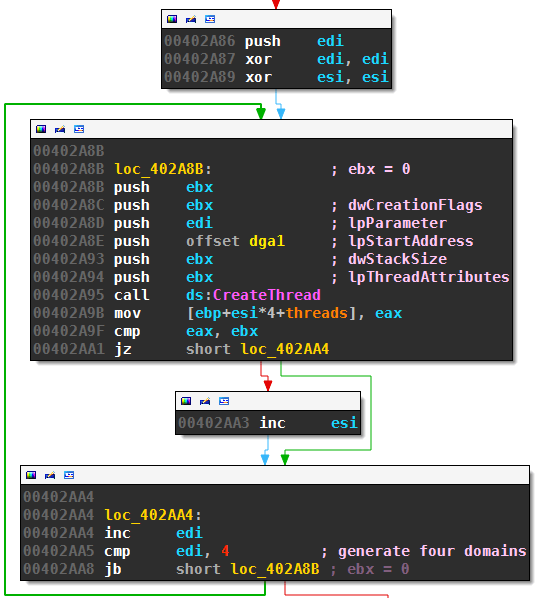
There is no delay between creating the threads, the four DNS queries happen at around the same time.
The Heart of the First DGA
Let’s see how the domains are generated by dga1:
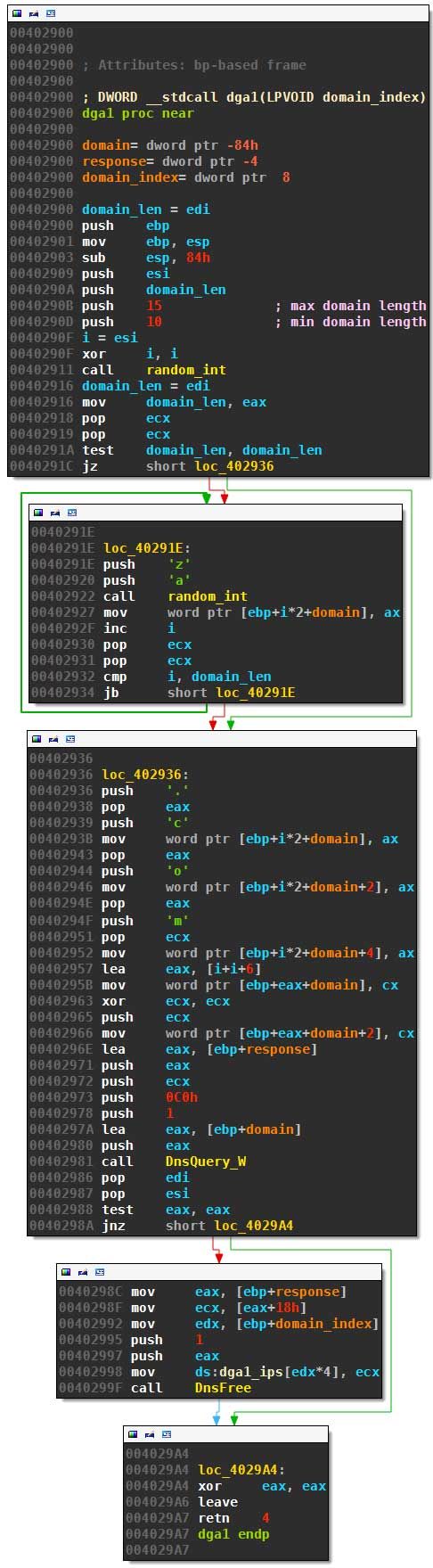
This very simple algorithm first randomly determines the length of the second level domain to be between 10 and 15 characters. It then builds the domain by picking uniformly at random from all lowercase letters and appending the hard-coded top level domain .com. The DGA concludes with querying the resulting domain; the resolved IP, if there is any, is appended to the array dga1_ips.
Pseudorandom Number Generator
The connectivity check, as well as dga1, use random_int to generate random integers. The disassembly of this routine is:
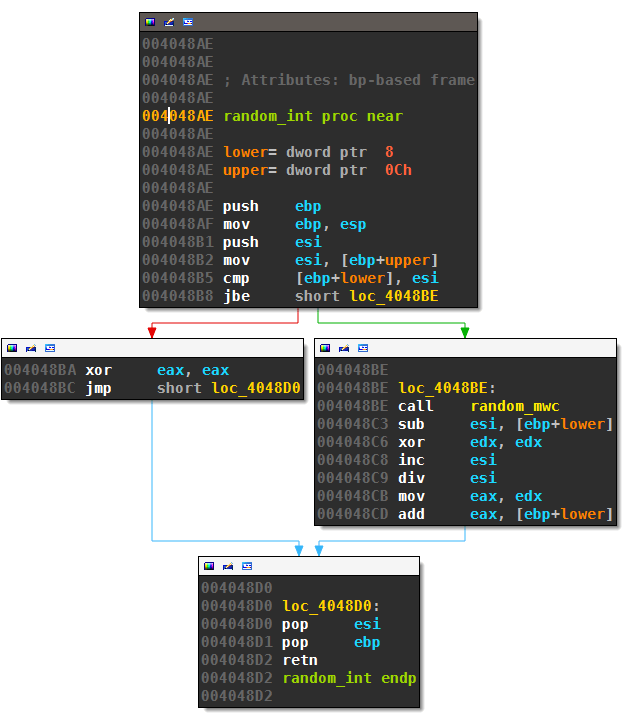
This is just a mapping of the return value of random_mwc to the desired range:
function random_int(lower, upper)
if lower > upper then
return 0
else
return lower + random_mwc % (upper - lower + 1)
The routine random_mwc is an almost standard implementation of a lag-3 multiply-with-carry pseudorandom number generator invented by George Marsaglia:
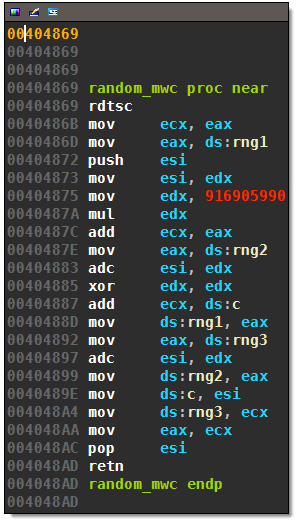
The only difference is the addition of an rdtsc summand, which will add the current time stamp counter to all generated numbers (not just the initial seed). The initial seed values and initial carry are:
0040F048 rng3 dq 77465321
0040F04C c dd 13579
0040F050 rng2 dd 362436069
0040F054 rng1 dd 123456789
The choice of these values is pretty common. Necurs never changed these values in its long existence according to the aforementioned article “the curse of Necurs”. This is the PRNG random_mwc in pseudo-code is:
b = 2^(32)
a = 916905990
// Initial seeds and carry
rng1 = 123456789
rng2 = 362436069
rng3 = 77465321
c = 13579
function random_mwc()
t = a*rng1 + rdtsc() + c
rng1 = rng2;
rng2 = rng3;
rng3 = t;
c = (t // b) % b
return v1;
The addition of rdtsc makes this random number generator, and therefore also the first domain generation algorithm, virtually impossible to predict.
Comparison with Facebook’s or Microsoft’s IP
Although the domains of dga1 are unusable as callback targets, they still serve a purpose: If one of the DGA IPs matches the one of Facebook or Microsoft (resolved during connectivity checking), Necurs will abort the callback attempt:
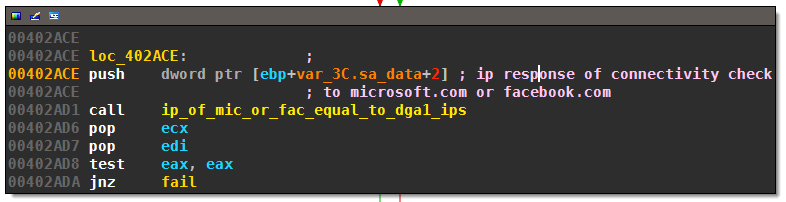
The excessively long named routine ip_of_mic_or_fac_equal_to_dga1_ips compares the IP of Microsoft or Facebook to the IPs of dga1 stored in array dga1_ips:
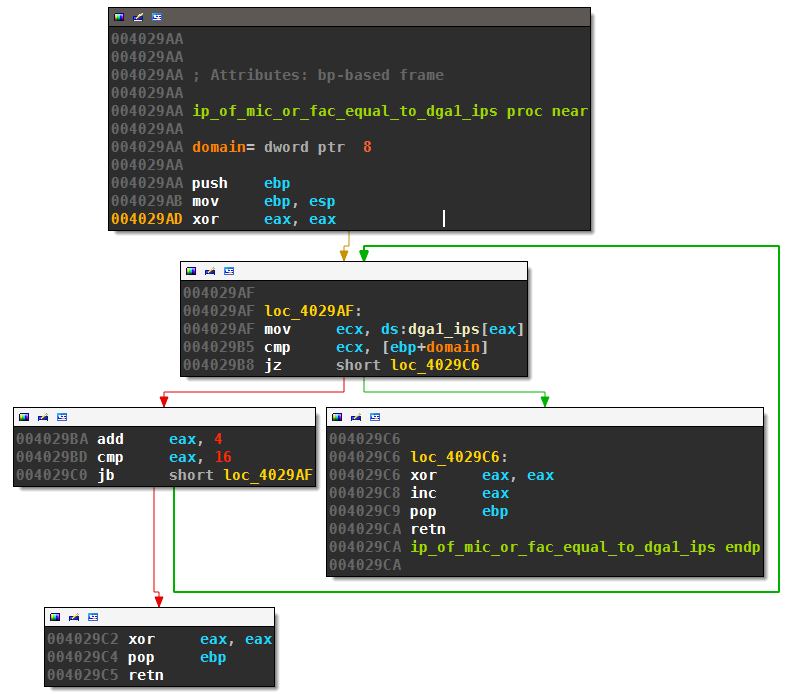
I suspect that Necurs tries to detect simulated internet services this way. Simulated Internet will typically return the same IP for all requested domains. The 4 DGA domains, however, are unpredictable and therefore non-existent. And even if the victim’s ISP uses DNS hijacking, the returned IPs will not match Facebook’s or Microsoft’s IP.
Summary
The first DGA of Necurs generates four .com domains of 10 to 15 lower case letters. It tries to resolve all four domains in parallel. The modified MWC-PRNG makes the domains unusable as callback targets; instead they are probably used to detect simulated internet connections in a lab environment.
The Second DGA
Necurs will continue without break with the second set of DGA domains in case the lab detection passed. The second set of DGA-like domains, for example qcmbartuop.bit, are not generated algorithmically but hard-coded. The following loop fetches 16 of those hard-coded domains and tries to contact them:
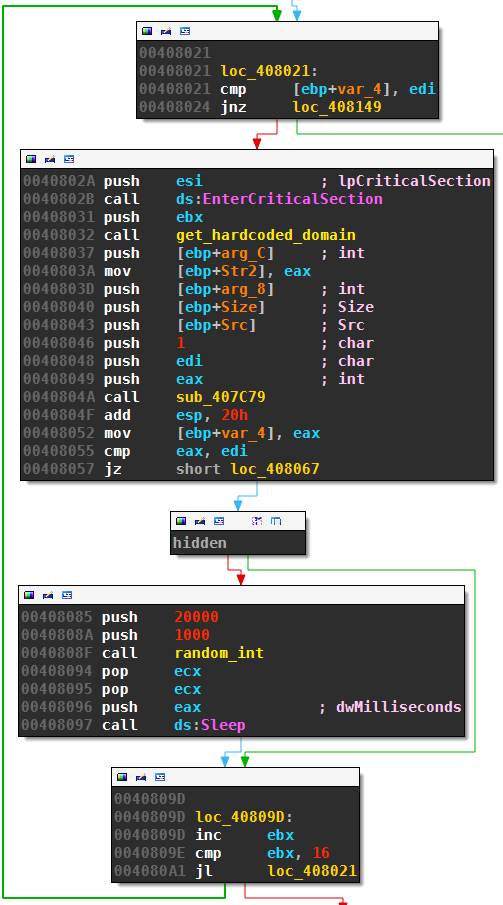
Necurs sleeps 1 to 20 seconds after each failed attempt, which sums up to a average total sleep time of about 5 minutes for all 16 attempts.
The relevant snippet of get_hard-coded_domain is:
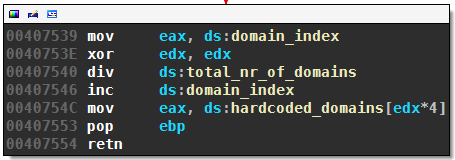
This returns the hard-coded domains one after another, starting over with the first domain if necessary.
From what I could gather from other reports, the hard-coded domains seem to mostly use the special .bit pseudo top level domain served by the namecoin project. The domains are probably Necurs` main C&C targets.
The Third DGA
If the second set of domains also fails to produce a working C&C server, Necurs tries one last set of domains.
Sequence Numbers
The third DGA starts by creating an array of 2048 sequence numbers 0 to 2047; these sequence numbers are then randomly permutated:
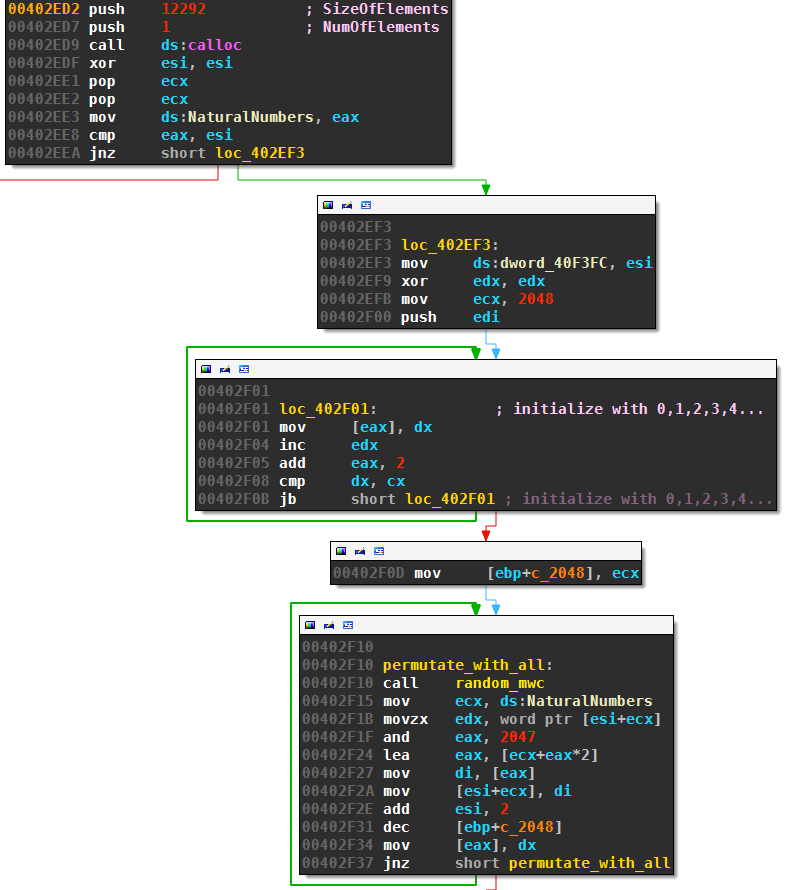
The permutation routine randomizes the sequence numbers in place with the following algorithm:
n = A.length
for i = 1 to n
swap A[i] with A[Random(1,n)]
Although this randomizes the sequence numbers, it does not do it uniformly. A better implementation would call Random(i,n) instead of Random(1,n), see for instance exercise 5.3-3 on page 129 of “Introduction to Algorithms”, 3rd edition. Nevertheless, the sequence numbers are still random and unpredictable because of the call to random_mwc which includes the current tick count see section above.
DGA Caller
After the sequence numbers have been randomized, Necurs starts up 16 threads, each with 128 of the sequence numbers (referenced by ecx, indexed by edi):
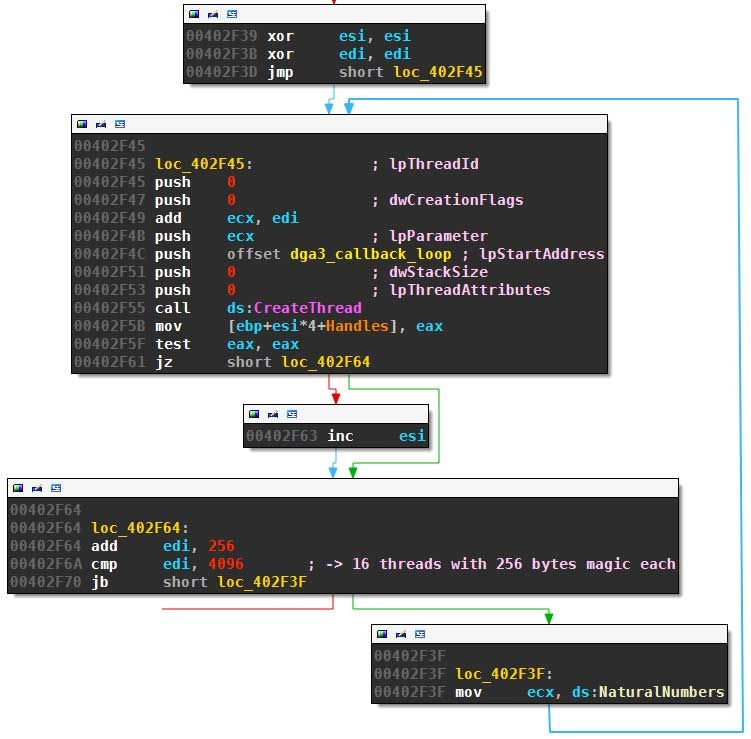
Each thread will call the routine to generates the domains for all 128 sequence numbers it got assigned to (unless a callback is successful beforehand):
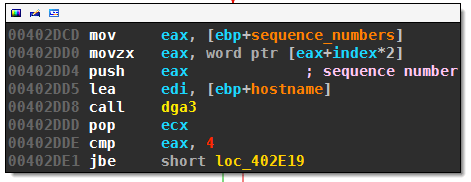
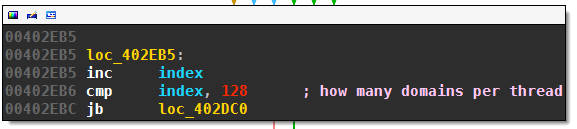
The DGA
At the heart of the third DGA we find this long, but easy to understand algorithm:
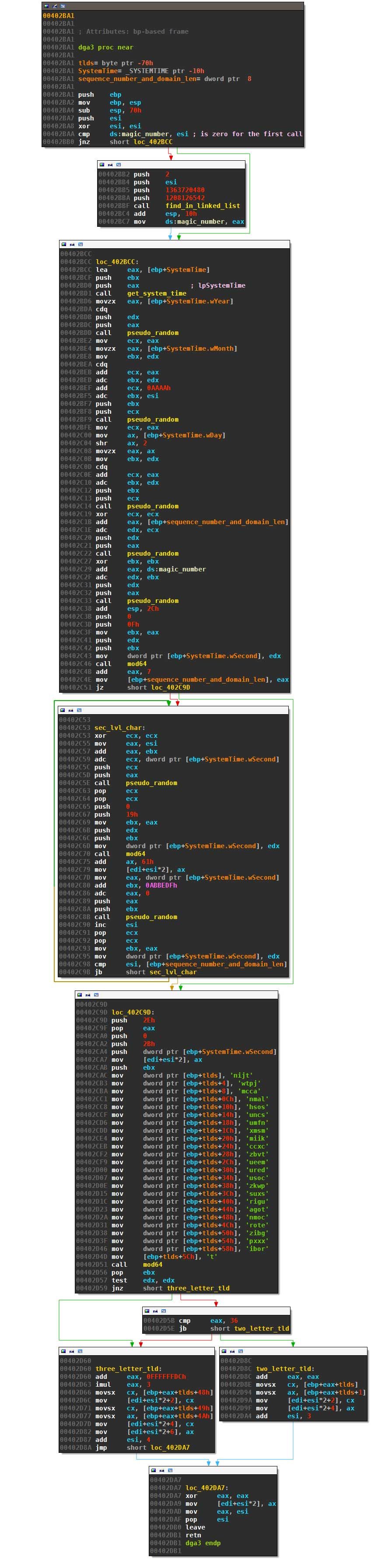
The first call to the routine fetches a hard-coded magic number from a rather complicated linked list and saves it as magic_number. For my sample, the hard-coded seed was 9.
Necurs then determines a length between 7 and 21 letters with multiple calls to pseudo_random, using the current date, the sequence number and the magic number as seeds. This will lead to a new set of domains every four days:
n = pseudo_random(date.year)
n = pseudo_random(n + date.month + 43690)
n = pseudo_random(n + (date.day>>2))
n = pseudo_random(n + sequence_nr)
n = pseudo_random(n + magic_nr)
domain_length = mod64(n, 15) + 7
Next, Necurs picks the characters of the second level domain from from ‘a’ to ‘y’ (‘z’ is unreachable like for Ramnit):
domain = ""
for i in range(domain_length):
n = pseudo_random(n+i)
ch = mod64(n, 25) + ord('a')
domain += chr(ch)
n += 0xABBEDF
n = pseudo_random(n)
Finally, one of 43 top level domains is chosen to finish the domain name:
tlds = ['tj','in','jp','tw','ac','cm','la','mn','so','sh','sc','nu','nf','mu',
'ms','mx','ki','im','cx','cc','tv','bz','me','eu','de','ru','co','su','pw',
'kz','sx','us','ug','ir','to','ga','com','net','org','biz','xxx','pro','bit']
tld = tlds[mod64(n, 43)]
domain += '.' + tld
return domain
All picks are randomized with calls to pseudo_random which is:
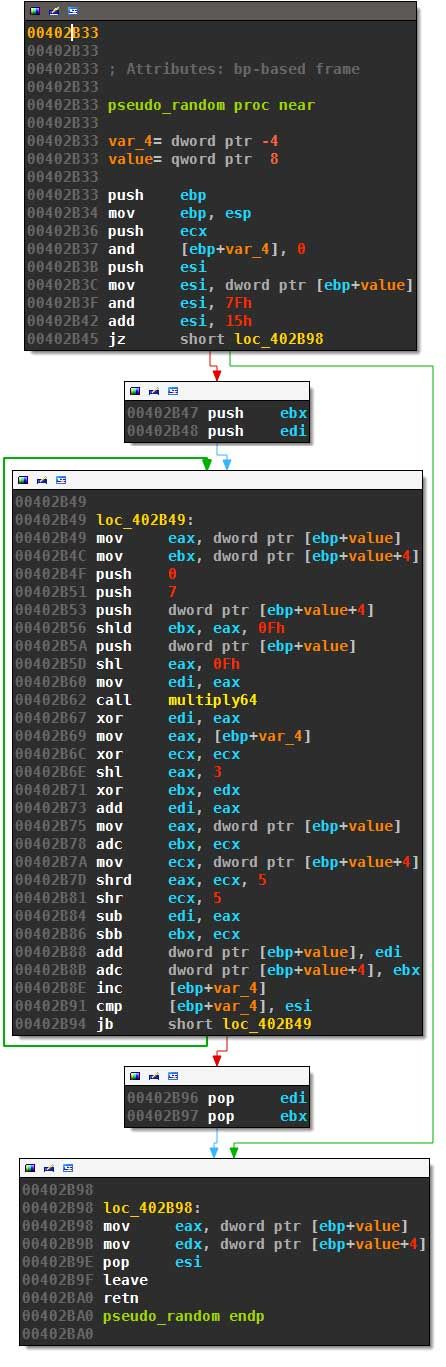
This routine calculates:
def pseudo_random(value):
loops = (value & 0x7F) + 21
for index in range(loops):
value += ((value*7) ^ (value << 15)) + 8*index - (value >> 5)
value &= ((1 << 64) - 1)
return value
Summary
The third DGA, including the random number generator, boils down to this routine:
import argparse
from datetime import datetime
def generate_necurs_domain(sequence_nr, magic_nr, date):
def pseudo_random(value):
loops = (value & 0x7F) + 21
for index in range(loops):
value += ((value*7) ^ (value << 15)) + 8*index - (value >> 5)
value &= ((1 << 64) - 1)
return value
def mod64(nr1, nr2):
return nr1 % nr2
n = pseudo_random(date.year)
n = pseudo_random(n + date.month + 43690)
n = pseudo_random(n + (date.day>>2))
n = pseudo_random(n + sequence_nr)
n = pseudo_random(n + magic_nr)
domain_length = mod64(n, 15) + 7
domain = ""
for i in range(domain_length):
n = pseudo_random(n+i)
ch = mod64(n, 25) + ord('a')
domain += chr(ch)
n += 0xABBEDF
n = pseudo_random(n)
tlds = ['tj','in','jp','tw','ac','cm','la','mn','so','sh','sc','nu','nf','mu',
'ms','mx','ki','im','cx','cc','tv','bz','me','eu','de','ru','co','su','pw',
'kz','sx','us','ug','ir','to','ga','com','net','org','biz','xxx','pro','bit']
tld = tlds[mod64(n, 43)]
domain += '.' + tld
return domain
if __name__=="__main__":
parser = argparse.ArgumentParser()
parser.add_argument("-d", "--date", help="as YYYY-mm-dd")
args = parser.parse_args()
date_str = args.date
if date_str:
date = datetime.strptime(date_str, "%Y-%m-%d")
else:
date = datetime.now()
for sequence_nr in range(2048):
print(generate_necurs_domain(sequence_nr, 9, date))
The characteristics of this DGA are:
| property | value |
|---|---|
| seed | magic number and current date (changing domains every four days) |
| domains per seed | 2048 |
| sequence | randomized (unpredictable, albeit not uniformly random) |
| wait time between domains | none, 16 parallel threads |
| top level domain | 43 different tld, picked randomly |
| second level characters | lower case letters except ‘z’ |
| second level domain length | 7 to 21 letters |
The DGA likely serves as a fallback in case the hard-coded domains fail.
Archived Comments
Note: I removed the Disqus integration in an effort to cut down on bloat. The following comments were retrieved with the export functionality of Disqus. If you have comments, please reach out to me by Twitter or email.
