Project Euler Problem 434 - Rigid graphs
Spoiler Alert! This blog entry gives away the solution to problem 434 of Project Euler. Please don’t read any further if you have yet to attempt to solve the problem on your own. The information is intended for those who failed to solve the problem and are looking for hints or test data to help them track down bugs.
First I provide references of the major theoretical background that you probably need to know to solve the problem and test data to validate your own algorithm. The last section presents the solution from start to finish.
The post reflects my approach to the problem. Even though the final outcome was accepted by Project Euler doesn’t mean the information is correct or elegant. Algorithms won’t necessarily be the most efficient ones, but they are guaranteed to run within the time limit of one minute.
Reference
You need to clear two hurdles to solve this problem:
- Find a representation of the grid where it is simple to determine if the grid is rigid or not.
- Calculate the number of stable grids
The first part is solvable without any special knowledge. But if you need help read this very nice introduction on the rigidity of grids.
The second part, finding an expression for the number of rigid grids, is very hard in my opinion. So you might also need to resort to literature. This paper delivers the magic formula. The paper reveals the answer to the first part of the Euler problem – don’t read it before you need to.
To make the algorithm run within the one minute time limit you might also need to know precomputation.
Test Data
| R(1,1) | 1 |
| R(1,2) | 1 |
| R(1,3) | 1 |
| R(1,4) | 1 |
| R(1,5) | 1 |
| R(2,2) | 5 |
| R(2,3) | 19 |
| R(2,4) | 65 |
| R(2,5) | 211 |
| R(3,3) | 205 |
| R(3,4) | 1795 |
| R(3,5) | 14221 |
| R(4,4) | 36317 |
| R(4,5) | 636331 |
| R(5,5) | 23679901 |
| S(10)mod1000000000033 | 990165545139 |
| S(20)mod1000000000033 | 446011381678 |
| S(50)mod1000000000033 | 643281900941 |
Solution
The Brace Graph
Regardless of how the grid is twisted and bent, the following holds:
- All vertical beams stay within a row
- All horizontal beams stay within a column
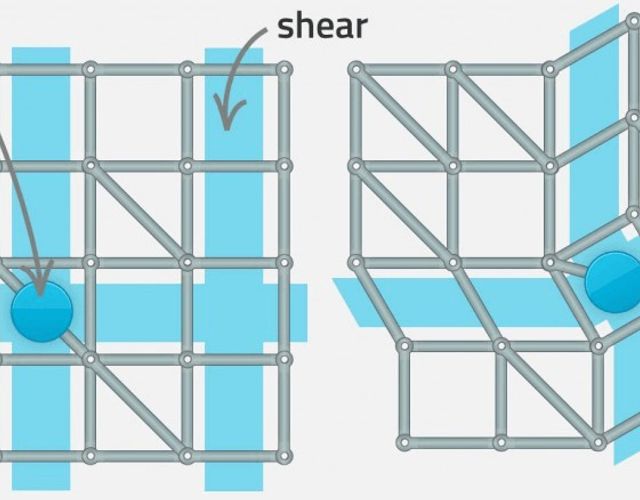
In the following graph, for example, the last column can shear. Furthermore, the graph can rotate around the marked cell. But all vertical (horizontal) bars within a row (column) stay parallel.
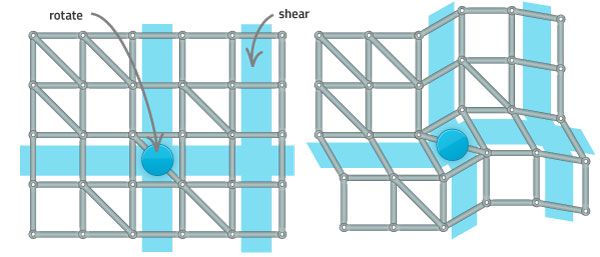
A diagonal beam added to a cell fixes the angle between the vertical beams and the horizontal beams of that cell to 90° – which means all vertical beams in the row (light blue) have a 90° angle to all horizontal beams (dark blue) in the column:

Let’s add another diagonal beam to a cell in the same row:
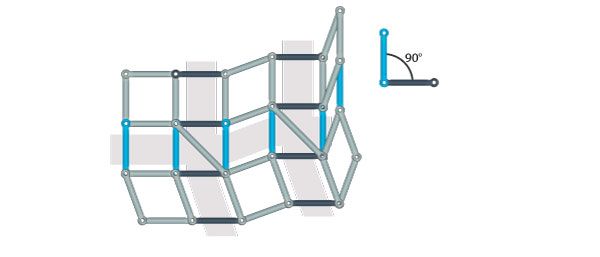
Now the horizontal beams in column x are perpendicular to the vertical beams in the selected row, which in turn are perpendicular to the horizontal beams in column y. As a consequence, the horizontal beams in the second and fourth column are parallel.
If the entire grid graph is supposed to be rigid, then all horizontal as well as all vertical beams need to be parallel. In other words, there needs to be a path of jumping from columns to rows to columns to rows and so forth that covers all rows and columns. To check that, the grid can be represented by the so called brace graph. Let the set of vertices U=u1,…,un represent all rows, and likewise V=v1,…,vn all columns. An edge connects ui and vj if cell (i,j) has a diagonal beam:
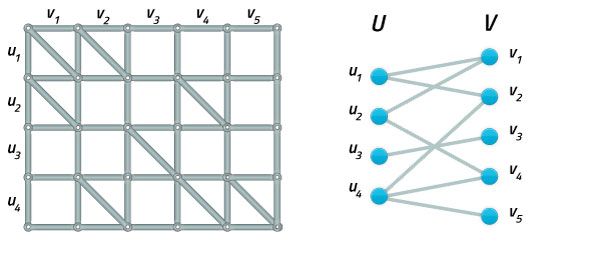
A grid is rigid, if all rows and all columns are connected, i.e., the corresponding beams are parallel. This corresponds to the bipartite graph being connected (as in the example above). All flexible grids on the other hand are represented by disconnected graphs, such as:

Count the Number of Rigid Grids
A grid is rigid if the corresponding brace graph is connected. The paper Labeled Bipartite Blocks derives a recurrsive relation for the number of connected labelled bipartite graphs:
R(i,j)=2ij−∑1≤a≤i0≤b≤ja<i∨b<j(i−1a−1)(jb)2(i−a)(j−b)R(a,b)
Algorithm
To speed up the algorithm, all powers of 2 up to N2 are precalculated. Also all coefficients (nr) are precalculated using the recurrence relation:
(nr)=(n−1k−1)+(n−1k)
from functools import lru_cache
@lru_cache(maxsize=None)
def R(i, j, m):
res = pof2[i*j]
for a in range(1,i+1):
for b in range(0, j+1):
if a == i and b == j:
continue
res = (res - nCr[i-1][a-1]*nCr[j][b]*\
pof2[(i-a)*(j-b)]*R(a, b, m)) % m
return res
def precompute(N, m):
# precompute 2^(i*j) for i*j <= N*N
global pof2
pof2 = [0 for i in range((N+1)*(N+1))]
pof2[0] = 1
for i in range(1,(N+1)*(N+1)):
pof2[i] = (pof2[i-1]*2) % m
# precompute n choose r for n,r < N
global nCr
nCr = [[0 for r in range(N+1)] for n in range(N+1)]
for i in range(N+1):
nCr[i][0] = 1
for n in range(1, N+1):
for r in range(1, N+1):
nCr[n][r] = (nCr[n-1][r-1] + nCr[n-1][r]) % m
def S(N, m):
# sum up all R (use R_ij = R_ji)
res = 0
for i in range(1, N+1):
for j in range(i, N+1):
f = 1 if i == j else 2
res += f*R(i, j, m) % m
return res % m
if __name__=="__main__":
m = 1000000033
N = 100
from datetime import datetime
startTime = datetime.now()
precompute(N,m)
print(S(N,m))
print("runtime: {0}".format( datetime.now()-startTime) )Archived Comments
Note: I removed the Disqus integration in an effort to cut down on bloat. The following comments were retrieved with the export functionality of Disqus. If you have comments, please reach out to me by Twitter or email.