Kraken's two Domain Generation Algorithms
A side by side comparison of the DGAs- December 22, 2015
- reverse engineering
- dga malware analysis
- no comments
- Reverse Engineering
- Pseudo Random Number Generator
- Seeding
- Discarding (only version 2)
- Length of Random Domain
- Building the Random Domain
- Base Domain
- Domain Counter
- Algorithm and Samples
- Python Implementations
- Version 1
- Version 2
- Properties of the DGA
- Samples
The DGA in this blog post has been implemented by the DGArchive project.
Kraken (also known as Oderoor or Bobax) was once a large, if not the largest, botnet. It was primarily used to send spam messages. Kraken features a Domain Generation Algorithm (DGA) which appeared in July 2007 and was first mentioned in 2008. This makes it one of the first ever widely used DGA.
The original DGA of Kraken is time-independent, i.e., a specific sample will at all times generate the same domains. There are various reports on how to determine the domains. Michael Ligh and Greg Sinclair showed how to use instrumented execution with Immunity debugger in their DEFCON 16 talk “Malware RCE: Debuggers and Decryptor Development” (skip to 18:24). The same method is also described in The Malware Analyst’s Cookbook, recipe 12-11 on page 476. This report by Damballa lists the domains for one parameterization of the DGA.
Much later — the first samples on Malwr are from 2003 — Kraken’s DGA changed. Probably recognizing the problem with generating the ever same domains, the authors added a time dependent input to the DGA. They also deviated from dynamic DNS providers and used four regular top level domains instead. A few samples, maybe from the transitional stage, still rely on the DDNS providers even with the new algorithm. Kraken infections with newer DGAs peaked in July 2014 (also see the list of samples in Section Samples).
The later version of Kraken’s DGA is much less reported on. Here is a analysis of the malware with the new domains. But neither the domains nor the domain generating algorithm are shown. For me, good enough grounds to look at both DGA in this short blog post. I’m aware that the DGA is irrelevant today, as Kraken is currently dead or inactive, but hopefully the post might still be interesting for the keen DGA historian.
Reverse Engineering
This section shows some reverse engineering insights of the DGA. Skip to Python Implementations to see reimplementations of the two algorithms.
Both the old and new version of the DGA have parameters that can change from sample to sample and cause disjoint sets of domains. I therefore looked at multiple samples to identify the variable parts of the DGA. For the old DGA I reversed two samples:
- source
- virusshare
- uploaded
- 2012-09-04 03:44
- SHA-256
- 5f004bd36715225c22ddb27d109a2b5f1c5215a6ce2df2e111c5fb49bc7161f9
- MD5
- 10fd78f9681d66d2dd39816b5f7f6ea6
and
- source
- malwr
- uploaded
- 2014-12-08 15:04
- SHA-256
- 4606a621922b28be1ff7f4621713aaafd988b8c5f1153720200c5e6dad0c5416
- MD5;
- 60838eeb3f8cd311de0faef80909632d
As far as the new version goes, I looked at these samples:
- source
- malwr
- uploaded
- 2013-08-05 04:16
- SHA-256
- 0fed48972c9b5c7fc6735db2b8764c45c95d45bde3764933b4a4909656c1ed47
- MD5
- f2ae73d866bb4edd14ee96cf74fbb423
and
- source
- virusshare
- uploaded
- 2012-04-12
- SHA-256
- e83bc2ec7975885424668171c2e106f7982bd409e01ce6281fb0e6e722e98810
- MD5
- 04966960f3f5ed32ae479079a1bcf6e9
All listed offsets are from the first sample respectively.
Pseudo Random Number Generator
Both Kraken’s DGA use a linear congruential generator (LCG) as pseudo random number generator (PRNG). The parameters are the same found in many rand() implementations:
rn+1=1103515245⋅rn+12435mod231
The bits 23 to 8 are used, i.e., r/256 mod 32768.
Seeding
The DGA of both versions first initializes the pseudo random number generator (PRNG). Two values are used to determine the seed of the PRNG:
- A running counter that starts at 0 and increases in steps of one (version 1) and one or two (version 2). In version 2 the increment depends on the outcome of the DNS response for the domain. The details of the counter are discussed in Section Domain Counter.
- Whether or not a list of hardcoded IPs could be contacted. These network connections are performed by
hardcoded_successat offsets001BE832and0x408D6Crespectively in the following images. The routine returnsTrueif the attempts were successful.
The following graph views are from the beginning of both DGAs. Both snippets initialize the random number — ecx in version 1 and ebx in version 2 — depending on the counter value and success of contact to hardcoded IPs. On left-hand side is the old version of the DGA, on the right-hand side the newer release (click to enlarge the images).
| version 1 | version 2 |
|---|---|
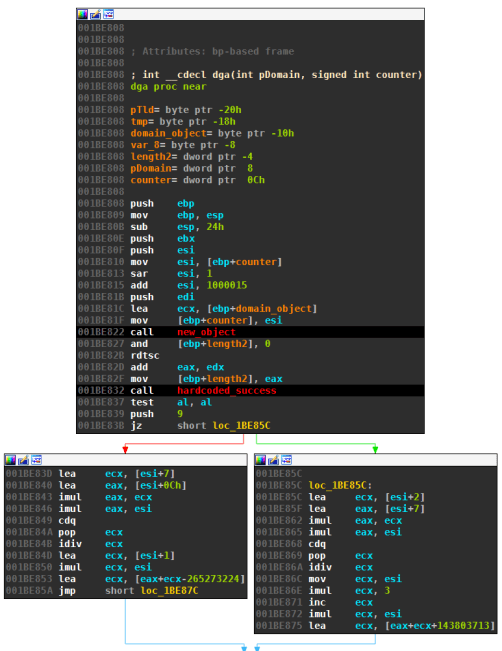 | 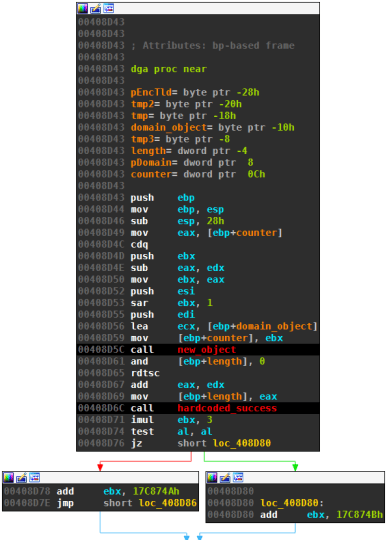 |
The hardcoded values -265273224 and 143803713 on the left, as well as -1FCFBF87h and 7924542h on the right might change from sample to sample. These parameters can be used to generate different sets of domains.
For the first version of the DGA, the snippet above boils down to the following, rather elaborate, formula:
d=⌊counter2⌋+1000015r={d⋅(d+7)⋅(d+12)/9+d⋅(d+1)+csif success with hardcoded IPsd⋅(d+2)⋅(d+7)/9+d⋅(3d+1)+cfotherwise
I found two different parameter sets. Notice that the changes are very subtle, only the first and last nibble vary:
| version 1 | cs | cf |
|---|---|---|
| Seed a | -0x0FCFBF88 | 0x8924541 |
| Seed b | -0x1FCFBF87 | 0x7924542 |
The second version uses a much simpler formula to initialize the random number:
d=⌊counter2⌋r=3d+{csif success with hardcoded IPscfotherwise
Again I found two parameter sets:
| version 2 | cs | cf |
|---|---|---|
| Seed a | 24938314 | 24938315 |
| Seed b | 1600000 | 1600001 |
Notice that in both versions the counter input to the DGA is first divided by two. The Malware Analyst’s Cookbook (page 480) considers this as a flaw of the DGA:
There are two weaknesses in Kraken’s DGA that are worth mentioning: (…) Odd numbers cause Kraken’s algorithm to generate the same domain names as the even numbers that precede them. This effectively cuts the number of possible domains generated by the DGA in half.
Section Domain Counter explains why I think this is by design and not a flaw of the DGA.
Discarding (only version 2)
Next follows code that is only present in the new version of Kraken’s DGA. The code incorporates a timestamp, which is determined by making an HTTP request to a randomly picked, legitimate website. The date is extracted from the http date header of the response and converted to unix timestamp format. For the analysed samples, the domains used to determine the time are: yahoo.com, google.com, live.com, msn.com, aol.com, amazon.com, go.com, bbc.co.uk, cnn.com, news.com, download.com, weather.com, comcast.net, mozilla.com and hp.com. The timestamp sets the variable discards:
| version 1 | version 2 |
|---|---|
| not present | 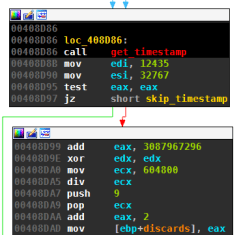 |
The divisor is the number of seconds in a week, so only every 7 days the value discard changes.
discards=⌊timestampunix−120700000024⋅7⋅3600⌋+2
The discard value, along with the current domain number, determines how many of the PRNG cycles are discarded:
| version 1 | version 2 |
|---|---|
| not present | 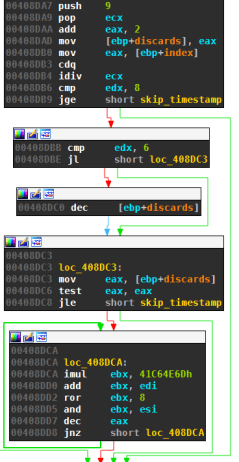 |
In Pseudocode this is:
discards = timestamp / 604800 + 2
IF domain_nr % 9 < 8
IF domain_nr % 9 >= 6
discards -= 1
REPEAT discards TIMES
r = rand(r)/256 % 32768
Notice that for every ninth domain discarding is skipped. Since the discards are the only time-dependent part of the DGA, those domains are invariants and prime targets for sinkholing.
Length of Random Domain
After the PRNG is initialized, the length of the random part of the domain is randomly picked. The two versions use almost the same algorithm:
| version 1 | version 2 |
|---|---|
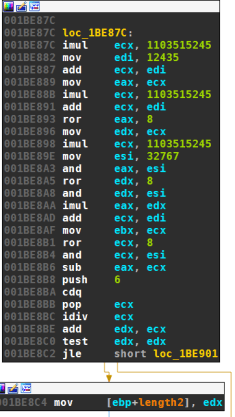 |
Both versions first generate three random numbers (ri is the random number after initialization and, for the second version, discarding):
ri+1=1103515245⋅ri+12435mod231ri+2=1103515245⋅ri+1+12435mod231ri+3=1103515245⋅ri+2+12435mod231
The first version uses the three random values to set the length as follows:
d(v1)length=⌊ri+1256mod32768⌋⌊ri+2256mod32768⌋−⌊ri+3256mod32768⌋mod6+6
The second version works almost the same, apart from (a) the third random number being added rather than subtracted and (b) the minimum length bein 7 instead of 6:
d(v2)length=⌊ri+1256mod32768⌋⌊ri+2256mod32768⌋+⌊ri+3256mod32768⌋mod6+7
This gives lengths between 6 and 11 characters for the first version, and 7 and 12 characters for the second version.
Building the Random Domain
Kraken uses straightforward calls to the random number generator to determine the characters of the random domain. All characters a-z are about equally likely picked. Both version use the exact same algorithm:
| version 1 | version 2 |
|---|---|
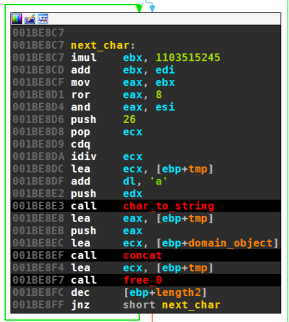 |
In Pseudocode this is:
domain = ""
REPEAT domain_length TIMES
r = rand(r)
domain += (r/256 % 32768) % 26 + 'a'
Base Domain
The final step of the domain generation algorithm is to append the base domain. For the first version, these base domains are four dynamic DNS providers. A few of the samples with the second DGA version use the same DDNS providers, for the most part the base domains are regular top level domains though. Domains are picked one after another from a hard-coded list:
| version 1 | version 2 |
|---|---|
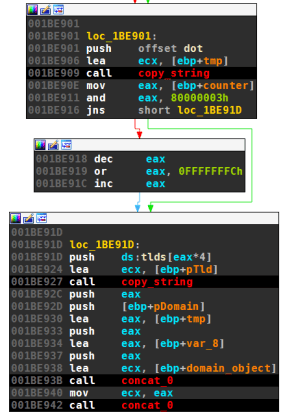 |  |
The base domains are:
- version 1, some version 2 samples
- “dyndns.org” → “yi.org” → “dynserv.com” → “mooo.com” (Free DDNS Providers)
- version 2
- “com” → “net” → “tv” → “cc” (Top Level Domains)
Domain Counter
As seen above, both DGA take a running counter as input. The counter starts at zero. Instead of an upper bound, the counter is reset after 30 minutes of trying to contact the C&C servers. There is some wait time between contacting domains which I did not examine; the expected number of generated domains is therefore unknown to me.
| version 1 | version 2 |
|---|---|
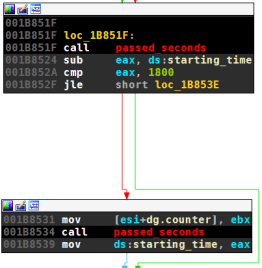 | 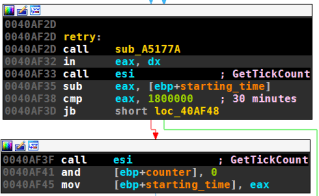 |
The old DGA always increments the index by one, regardless of the call-home attempt for the generated domains. For version 2 things are a little more complicated; the DGA can increment the counter by one or two:
| version 1 | version 2 |
|---|---|
 |  |
The counter in version 2 is incremented depending on the DNS response to the generated domain. The IP is compared to various hard-coded domains. For example:
0040AFB9 cmp eax, 127 ; eax first tuple of IP
0040AFBC jz short private_ip
0040AFBE
0040AFBE loc_40AFBE:
0040AFBE cmp eax, 192
0040AFC3 jnz short loc_40AFCD
0040AFC5 cmp ecx, 168
0040AFCB jz short private_ip
0040AFCD
0040AFCD loc_40AFCD:
0040AFCD cmp eax, 172
0040AFD2 jnz short loc_40AFDE
0040AFD4 cmp ecx, 16 ; ecx second tuple of IP
0040AFD7 jl short loc_40AFEB
0040AFD9 cmp ecx, 31
0040AFDC jle short private_ip
...
All IPs from the following list are treated specially (I do not know why 66.116.125.150 and 72.51.27.51 get special treatments, maybe those were sinkholes in the past).
| range | comment |
|---|---|
| 127.x.x.x | reserved range |
| 192.168.x.x | reserved range |
| 172.16.0.0 - 172.31.255.255 | reserved range |
| 0.x.x.x | includes failed queries |
| 1.1.1.1, 2.2.2.2, … , 255.255.255.255 | unlikely answers? Sandbox detection? |
| 66.116.125.150 | IP in US |
| 72.51.27.51 | IP in Canada |
If the IP matches with one of above the subnets, the counter grows to the next multiple of two, i.e., even counters are increased by two, and odd counters are increased one.
Since inside the DGA routine, odd counters are rounded down to the same number as their previous (even) counters, every domain that returned an IP that was not in a “blacklisted” range will be checked twice. I, for one, don’t think that’s a flaw of the DGA, but a — overly complicated — way to recheck domains.
Algorithm and Samples
Python Implementations
Version 1
The following Python Code generates 1000 domains for a provided seed (either a or b). The code alternately generates domains for when the hardcoded IP callback failed and succeeded.
import time
from ctypes import c_int, c_uint
import argparse
def rand(r):
t = c_int(1103515245 * r + 12435).value
return t
def crop(r):
return (r // 256) % 32768
def dga(index, seed_set, temp_file=True):
seeds = {'a': {'ex': -0x0FCFBF88, 'nex': 0x8924541},
'b': {'ex': -0x1FCFBF87, 'nex': 0x7924542}}
tlds = ["dyndns.org", "yi.org", "dynserv.com", "mooo.com"]
domain_nr = int(index/2) + 1000015
if temp_file:
x = int(c_int(domain_nr*(domain_nr + 7)*(domain_nr+12)).value /9.0)
y = domain_nr*(domain_nr+1)
r = c_int(x + y + seeds[seed_set]['ex']).value
else:
x = int(c_int((domain_nr + 2)*(domain_nr + 7)*domain_nr).value/9.0)
y = (domain_nr*3 + 1)*domain_nr
r = c_int(x + y + seeds[seed_set]['nex']).value
rands = 3*[0]
for i in range(3):
r = rand(r)
rands[i] = crop(r)
domain_length = (rands[0]*rands[1] - rands[2]) % 6 + 6
domain = ""
for i in range(domain_length):
r = rand(r)
ch = crop(r) % 26 + ord('a')
domain += chr(ch)
domain += "." + tlds[domain_nr % 4]
return domain
def get_domains(nr, seed_set):
domains = []
for i in range(nr):
for temp_file in range(2):
domains.append(dga(i*2, seed_set, temp_file))
return domains
if __name__=="__main__":
parser = argparse.ArgumentParser()
parser.add_argument('-s', '--seed', choices=['a','b'], default='a')
args = parser.parse_args()
for domain in get_domains(1000, args.seed):
print(domain)
For example:
$ python dga_v1.py -s b
hmhxnupkc.mooo.com
quowesuqbbb.mooo.com
rffcteo.dyndns.org
adrcgmzrm.dyndns.org
bdubefoeug.yi.org
bpdyttrlp.yi.org
hovdworcxd.dynserv.com
dljemwae.dynserv.com
nlnylxvrbel.mooo.com
dcdkfq.mooo.com
gyuzohut.dyndns.org
lfiavsbyntu.dyndns.org
waxmtzkqblh.yi.org
zvfctvkdng.yi.org
hshfmrobfjr.dynserv.com
uaqjtycx.dynserv.com
prifhjstv.mooo.com
csukibyyt.mooo.com
ghcxncadnj.dyndns.org
iskqszufrft.dyndns.org
These are also the domains from The Malware Analyst’s Cookbook.
Version 2
The second DGA also takes the current date and top level set
import time
import argparse
from datetime import datetime
def rand(r):
t = (1103515245 * r + 12435) & 0xFFFFFFFF
return t
def crop(r):
return (r // 256) % 32768
def dga(index, date, seed_set, temp_file=True, tld_set_nr=1):
tld_sets = {1: ["com", "net", "tv", "cc"],
2: ["dyndns.org", "yi.org", "dynserv.com", "mooo.com"]}
seeds = {'a': {'ex': 24938314 , 'nex': 24938315 },
'b': {'ex': 1600000, 'nex': 1600001}}
tlds = tld_sets[tld_set_nr]
domain_nr = int(index/2)
if temp_file:
r = 3*domain_nr + seeds[seed_set]['ex']
else:
r = 3*domain_nr + seeds[seed_set]['nex']
discards = (int(time.mktime(date.timetuple())) - 1207000000) // 604800 + 2
if domain_nr % 9 < 8:
if domain_nr % 9 >= 6:
discards -= 1
for _ in range(discards):
r = crop(rand(r))
rands = 3*[0]
for i in range(3):
r = rand(r)
rands[i] = crop(r)
domain_length = (rands[0]*rands[1] + rands[2]) % 6 + 7
domain = ""
for i in range(domain_length):
r = rand(r)
ch = crop(r) % 26 + ord('a')
domain += chr(ch)
domain += "." + tlds[domain_nr % 4]
return domain
def get_domains(nr, date, seed, tld_set):
domains = []
for i in range(nr):
for temp_file in range(2):
domains.append(dga(i*2, date, seed, temp_file, tld_set))
return domains
if __name__=="__main__":
parser = argparse.ArgumentParser()
parser.add_argument("-d", "--date",
help="date for which to generate domains")
parser.add_argument("-t", "--tld", choices=[1,2], type=int,
help="tld set", default=1)
parser.add_argument('-s', '--seed', choices=['a','b'], default='a')
args = parser.parse_args()
if args.date:
d = datetime.strptime(args.date, "%Y-%m-%d")
else:
d = datetime.now()
for domain in get_domains(1000, d, args.seed, args.tld):
print(domain)
For example:
$ python dga_v2.py -d 2013-12-12 -t 1 -s a
gwbgmsmhgsp.com
bizyssylscs.com
egbmbdey.net
ogoqxbevdeqm.net
iuhqhbmq.tv
iuhqhbmq.tv
wedlgyvplmt.cc
zoipmnwr.cc
gktdtghza.com
toogdpdiekwh.com
iuhqhbmq.net
oxfjukumll.net
vwmlcid.tv
glmvhcm.tv
pgmryukdb.cc
egbmbdey.cc
vsdvzwt.com
wixcaiktigew.com
xewokii.net
lvctmusxcyz.net
You also find the code on my GitHub page.
Properties of the DGA
The properties of the two DGAs are:
| version 1 | version 2 | |
|---|---|---|
| time dependent | no | yes |
| granularity | - | 1 week |
| domains per seed and day | variable, as many as can be generated in 30 minutes | see version 1 |
| sequence | sequential | see version 1 |
| wait time between domains | unknown | see version 1 |
| top level domains | .dyndns.org, yi.org, dynserv.com, mooo.com | some as version 1, but mostly com, .net, .tv, .cc |
| second level characters | lower case a-z | see version 1 |
| second level domain length | 6 to 11 | 7 to 12 |
Samples
The following table shows reports on malwr.com that contact at least one domain generated by the second version of Kraken’s DGA. Many samples seem to be downloader, e.g., Vobfus, and the domains are actually generated by the Kraken payload.
| md5 | analysis date | tlds | Microsoft | Kaspersky | Sophos |
|---|---|---|---|---|---|
| 04966960f3f5ed32ae479079a1bcf6e9 | 16 Jul. 2013 | 1A | 1Oderoor.gen!C | Email-Worm.Win32.Agent.fe | 2EncPk-DJ |
| f2ae73d866bb4edd14ee96cf74fbb423 | 05 Aug. 2013 | 1A | Clean | 3Generic | 1Generic-S |
| c13abb6be8a1c7fc9b18c8fd0a9488b7 | 09 Oct. 2013 | 1A | 4Rimecud.A | 2Generic | 5Rimecud-DD |
| c13abb6be8a1c7fc9b18c8fd0a9488b7 | 10 Oct. 2013R | 1A | 3Rimecud.A | 2Generic | 4Rimecud-DD |
| 1ec55311a564f8272d62ccb621a8b513 | 22 Oct. 2013 | 1A | 3Sisron | 6Agent.hdqc | 1EncPk-CK |
| 1ec55311a564f8272d62ccb621a8b513 | 28 Nov. 2013R | 1A | 3Sisron | 5Agent.hdqc | 1EncPk-CK |
| 1ec55311a564f8272d62ccb621a8b513 | 18 Dec. 2013R | 1A | 3Sisron | 5Agent.hdqc | 1EncPk-CK |
| 04966960f3f5ed32ae479079a1bcf6e9 | 24 Jan. 2014R | 2B | 0Oderoor.gen!C | 2Generic | 1EncPk-DJ |
| 1ec55311a564f8272d62ccb621a8b513 | 24 Jan. 2014R | 1A | 3Sisron | 5Agent.hdqc | 1EncPk-CK |
| 1ec55311a564f8272d62ccb621a8b513 | 25 Jan. 2014R | 1A | 3Sisron | 5Agent.hdqc | 1EncPk-CK |
| 04966960f3f5ed32ae479079a1bcf6e9 | 27 Jan. 2014R | 2B | 0Oderoor.gen!C | 2Generic | 1EncPk-DJ |
| 1ec55311a564f8272d62ccb621a8b513 | 05 Feb. 2014R | 1A | 3Sisron | 5Agent.hdqc | 1EncPk-CK |
| 1ec55311a564f8272d62ccb621a8b513 | 13 Feb. 2014R | 1A | 3Sisron | 5Agent.hdqc | 1EncPk-CK |
| 1ec55311a564f8272d62ccb621a8b513 | 21 Feb. 2014R | 1A | 3Sisron | 5Agent.hdqc | 1EncPk-CK |
| c7ec51ac3b9d91a483f1860c3d965f16 | 03 Mar. 2014 | 1A | Clean | 2Generic | 1Generic-S |
| c7ec51ac3b9d91a483f1860c3d965f16 | 17 Mar. 2014R | 1A | 0Oderoor.M | 2Generic | 1Generic-S |
| c7ec51ac3b9d91a483f1860c3d965f16 | 19 Mar. 2014R | 1A | 0Oderoor.M | 2Generic | 1Generic-S |
| c7ec51ac3b9d91a483f1860c3d965f16 | 25 Mar. 2014R | 1A | 0Oderoor.M | 2Generic | 1Generic-S |
| c7ec51ac3b9d91a483f1860c3d965f16 | 01 Apr. 2014R | 1A | 0Oderoor.M | 2Generic | 4Agent-AGLO |
| c7ec51ac3b9d91a483f1860c3d965f16 | 22 Apr. 2014R | 1A | Clean | 5Agent.hegf | 4Agent-AGLO |
| c413f1a0738a3b475db2ed44aecbf3ba | 16 Jun. 2014 | 1A | 0Oderoor.M | 2Generic | 1EncPk-CK |
| 0bfd909d651a11e3d3cdf5b091ee12a1 | 28 Jun. 2014 | 1A | 7Vobfus | 8Win32.Agent.agdmx | 1SillyFDC-S |
| 15993254499407fd7cbe701be11106f1 | 01 Jul. 2014 | 1A | 6Vobfus.ZV | 7Win32.Agent.ageop | 1SillyFDC-S |
| 1598723f88c6432e8ceee68336a08b01 | 01 Jul. 2014 | 1A | 6Vobfus | 7Win32.Agent.agcvt | 1VB-ALW |
| 17d4b6b618f7576023dd3b983416a180 | 01 Jul. 2014 | 1A | 6Vobfus | Worm.Win32.Vobfus.escx | 1VB-ALW |
| 1bfac857a733ec498fc1efc0ebb6a236 | 02 Jul. 2014 | 1A | 6Vobfus.ZO | 7Win32.Agent.agcnq | 1VB-ALW |
| 1cfb3882d79b42f2f881ea20cca0f780 | 02 Jul. 2014 | 1A | 6Vobfus | Worm.Win32.Vobfus.esdv | 1VB-ALW |
| 1e291e57c007acd5aecbcddd156c46e6 | 02 Jul. 2014 | 1A | 6Vobfus | Worm.Win32.Vobfus.escj | 1SillyFDC-S |
| 1fafa36c436af003b28fd9d7befddf01 | 02 Jul. 2014 | 1A | 6Vobfus | 7Win32.Agent.agerc | 1SillyFDC-S |
| 20ff4c7b6265bc2b7e9b66bbfe4c8ee6 | 02 Jul. 2014 | 1A | 6Vobfus.ZZ | Worm.Win32.Vobfus.esdw | 1VB-ALW |
| 22a5ce2602e8a0f76e4ab1db713098c6 | 03 Jul. 2014 | 1A | 6Vobfus | Worm.Win32.Vobfus.esaj | 1VB-ALW |
| 26e7996626da3fbf66b78c0b5969efc1 | 03 Jul. 2014 | 1A | 6Vobfus.ZM | 7Win32.VBKrypt.urjq | 1VB-ALW |
| 272577cdcd11389a4b95d5eae8f3c5b1 | 04 Jul. 2014 | 1A | 6Vobfus.ZW | 7Win32.Agent.agexl | 1SillyFDC-S |
| 27549feb774b058fde65bc3936a0bf36 | 04 Jul. 2014 | 1A | 6Vobfus | 7Win32.Agent.agcvt | 1VB-ALW |
| 2807aafab5a799ff261b3f614aecbf91 | 04 Jul. 2014 | 1A | 6Vobfus.ZC | Worm.Win32.Vobfus.erwz | 1SillyFDC-AH |
| 2812ce13236087c1a5b30f63ae33c7a0 | 04 Jul. 2014 | 1A | 6Vobfus.ZW | 7Win32.Agent.agexl | 1SillyFDC-S |
| 2825b9e636ad7a9304ea97981b68bf20 | 04 Jul. 2014 | 1A | 6Vobfus.YS | 7Win32.VBKrypt.uqif | 1SillyFDC-AH |
| 292028779b7c4c2e525ccbad0e0f5161 | 04 Jul. 2014 | 1A | 6Vobfus | 7Win32.Agent.agere | 1SillyFDC-S |
| 2bc4df2819c8983b1511814809c2c641 | 04 Jul. 2014 | 1A | 6Vobfus | Worm.Win32.Vobfus.esdv | 1VB-ALW |
| 28d89ceb348459fd7d1468e130b1a706 | 04 Jul. 2014 | 1A | 6Vobfus.ZD | Worm.Win32.Vobfus.erxc | 1SillyFDC-AH |
| 2c3b96ca3a18140dfcd42434f3e03020 | 04 Jul. 2014 | 1A | 6Vobfus.ZQ | Worm.Win32.Vobfus.erzx | 1VB-ALW |
| 2c931871fef3b50c0bd2b4961419a311 | 04 Jul. 2014 | 1A | 6Vobfus | Worm.Win32.Vobfus.esat | 1VB-ALW |
| 2cae6bd4e939b318726eebb347db0a26 | 04 Jul. 2014 | 1A | 6Vobfus.ZW | 7Win32.Agent.agexl | 1SillyFDC-S |
| 2cc5ad6770250338bd5844904fb18181 | 04 Jul. 2014 | 1A | 6Vobfus | 7Win32.Agent.agcsv | 1VB-ALW |
| 2d07ba427df9cd2c4af815015a484391 | 04 Jul. 2014 | 1A | 6Vobfus.YY | Worm.Win32.Vobfus.ervr | 1SillyFDC-S |
| 2d321324e9a28c834a750860122233c6 | 04 Jul. 2014 | 1A | 6Vobfus | 7Win32.Agent.agcvt | 1VB-ALW |
| 2db1a991aea1664e3dcbc5e75e108131 | 04 Jul. 2014 | 1A | 6Vobfus | Worm.Win32.Vobfus.erwv | 1Generic-S |
| 2f2a752f96ecb251efdc275f0ec8ea80 | 04 Jul. 2014 | 1A | 6Vobfus.ZV | ? | 1SillyFDC-S |
| 2fab042f7b482e8aa2c5ecd413f2eff1 | 05 Jul. 2014 | 1A | 6Vobfus | 7Win32.Agent.agcvt | 1VB-ALW |
| 2fcae2e2a9ed2f36bd399c77da2470c6 | 05 Jul. 2014 | 1A | 6Vobfus.ZW | 7Win32.Agent.agexl | 1SillyFDC-S |
| 30cc569d95b4401aa0681b8e01299981 | 05 Jul. 2014 | 1A | 6Vobfus.YU | ? | ? |
| 30cf2bf448db73c75e153216d4cd4fc0 | 05 Jul. 2014 | 1A | 6Vobfus | 7Win32.VBKrypt.uron | 1SillyFDC-S |
| 302471280652d2d1817757ef0f8ad656 | 05 Jul. 2014 | 1A | 6Vobfus | Worm.Win32.Vobfus.esdv | 1VB-ALW |
| 3127e3127a2a206a8dc6bc21f4693386 | 05 Jul. 2014 | 1A | 6Vobfus.ZW | 7Win32.Agent.agexl | 1SillyFDC-S |
| 33bf61ebeb41d157b45d3180d1f71b76 | 05 Jul. 2014 | 1A | 6Vobfus.ZN | 7Win32.VBKrypt.urkc | 1VB-ALW |
| 33c739e7d6aa599c05ff9f94a5768921 | 05 Jul. 2014 | 1A | 6Vobfus.ZR | 7Win32.Agent.agcpv | 1VB-ALW |
| 32d5e945a82fb6fb511e7bdd32cf8c21 | 05 Jul. 2014 | 1A | 6Vobfus | Worm.Win32.Vobfus.eseu | 1Generic-S |
| 34defe58f6d305960fff8c295bd9b851 | 05 Jul. 2014 | 1A | 6Vobfus.ZW | ? | 1SillyFDC-S |
| 383977446a2a42bd1427703974265606 | 06 Jul. 2014 | 1A | 6Vobfus.ZW | 7Win32.Agent.agexl | 1SillyFDC-S |
| 39408e199dd996cbe915c5c32261c490 | 06 Jul. 2014 | 1A | 6Vobfus.ZN | 7Win32.VBKrypt.urkc | 1VB-ALW |
| 395df008604e98e228ed41ce67f213b1 | 06 Jul. 2014 | 1A | 6Vobfus.ZV | 7Win32.Agent.ageop | 1SillyFDC-S |
| 3d6d6bbe37b37be79c43dc6a7b052a46 | 06 Jul. 2014 | 1A | 6Vobfus | 7Win32.Agent.agere | 1SillyFDC-S |
| 38ab4d2cda29c4ba1346da4b85c81800 | 06 Jul. 2014 | 1A | 6Vobfus.ZW | 7Win32.Agent.agexl | 1SillyFDC-S |
| 3ca13a5648d4f2573f28b37638333701 | 06 Jul. 2014 | 1A | 6Vobfus.YF | 7Win32.VBKrypt.uprs | 1SillyFDC-AH |
| 3bc39b3af9f13317744fd0548503baa6 | 07 Jul. 2014 | 1A | 6Vobfus.YU | Worm.Win32.Vobfus.erwm | 1VB-ALR |
| c413f1a0738a3b475db2ed44aecbf3ba | 30 Sep. 2014R | 1A | 0Oderoor.M | Clean | 1EncPk-CK |
| 675d97e5cdd3b7e07c7945fa5398e599 | 21 May. 2015 | 1A | ? | ? | ? |
Prefixes: 0Backdoor:Win32/, 1Mal/, 2HEUR:Trojan.Win32., 3Trojan:Win32/, 4Troj/, 5Trojan-Downloader.Win32., 6Worm:Win32/, 7Trojan.
TLDS: A com, net, tv, cc. Bdyndns.org, yi.org, dynserv.com, mooo.com
