Crackmes.de – gama’s mndg
- October 28, 2014
- reverse engineering
- crackmes
- no comments
This crackme is rated Difficulty: 2 – Needs a little brain (or luck). Although it is an easier crackme and it was published almost half a year ago, there are no accepted solutions yet. There are many comments for this crackme with people who solved this crackme, however, they all used some kind of brute forcing or even patching. This solutions show how to generate serials mathematically. If you run the crackme without debugger and enter an invalid serial, you get the dialog box shown in the following screenshot:
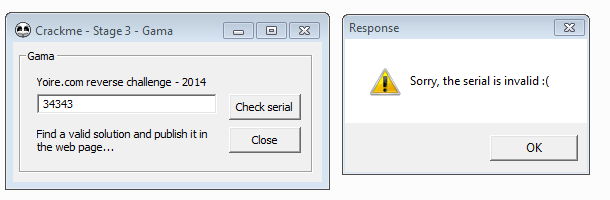
If you run the crackme with a debugger like OllyDbg (or attach to the running process), entering an invalid serial will most likely lead to a memory access violation similar to this:

This crackme uses Anti-Debugging techniques. The first part of this solution discusses the two anti-debugging tricks of this crackme and how to remove those check with patches.
Anti-Debugging
Finding the subroutine that checks the serial is trivial: search for the string “Sorry, the serial is invalid :(” and you get the following clean code sequence:
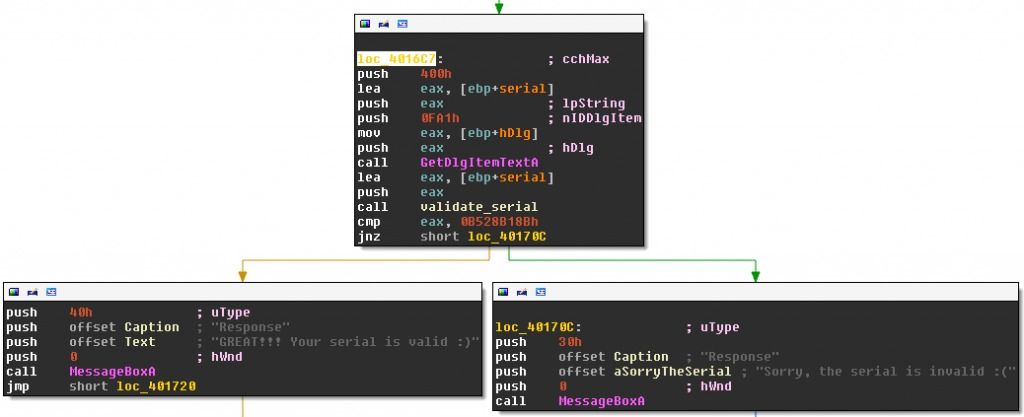
The subroutine at dword_405000 – I renamed it to validate_serial- is clearly calculating a value based on the serial. If the return value of validate_serial is 0xB528B18B, then the serial is valid, otherwise it is invalid. The subroutine validate_serial is located at an unusual place:
.data:00405000 validate_serial dd 8000000h
Offset 0x80000000 is far from the image base and likely created during runtime. Here is the disassembly of validate_serial when it is called first:
debug138:08000000 push edx debug138:08000001 mov al, [ebp+25h] debug138:08000004 or dword_101BFEC[ebx], edi debug138:0800000A jmp far ptr 4E0h:0C0D08815h
This doesn’t look like valid code, and will probably lead to the memory access violation exceptions shown before. If we would have run the crackme without debugger, then offset 0x80000000 probably looks different. First, let`s find the code location that creates and writes offset 0x8000000. We find the relevant code segment by looking for tale-tale API calls to VirtualAlloc with starting address 0x80000000. Here is the code snippet that allocates the memory and probably writes to it in sub_4015A0:
.text:00401633 push 40h ; flProtect .text:00401635 push 3000h ; flAllocationType .text:0040163A push 10000h ; dwSize .text:0040163F push 8000000h ; lpAddress .text:00401644 call VirtualAlloc .text:0040164A call sub_4015A0 .text:0040164F mov [ebp+var_82B], al .text:00401655 xor esi, esi .text:00401657 jmp short loc_40167D
Let’s dive into sub_4015A0 and look for anti-debugging measures.
OllyDbg.exe
Inside sub_4015A0, we find the following loop:
.text:004015A0 sub_4015A0 proc near ; CODE XREF: DialogFunc+6Ap .text:004015A0 .text:004015A0 olly_dbg = byte ptr -0Ch .text:004015A0 var_1 = byte ptr -1 .text:004015A0 .text:004015A0 push ebp .text:004015A1 mov ebp, esp .text:004015A3 sub esp, 0Ch .text:004015A6 lea ecx, [ebp+olly_dbg] .text:004015A9 mov edx, offset unk_404074 .text:004015AE mov eax, [edx] .text:004015B0 mov [ecx], eax .text:004015B2 mov eax, [edx+4] .text:004015B5 mov [ecx+4], eax .text:004015B8 mov eax, [edx+8] .text:004015BB mov [ecx+8], eax .text:004015BE xor eax, eax .text:004015C0 jmp short loc_4015C8 .text:004015C2 ; --------------------------------------------------------------------------- .text:004015C2 .text:004015C2 loc_4015C2: ; CODE XREF: sub_4015A0+2Bj .text:004015C2 xor [ebp+eax+olly_dbg], 81h .text:004015C7 inc eax .text:004015C8 .text:004015C8 loc_4015C8: ; CODE XREF: sub_4015A0+20j .text:004015C8 cmp eax, 0Ch .text:004015CB jb short loc_4015C2 .text:004015CD mov [ebp+var_1], 0 .text:004015D1 lea eax, [ebp+olly_dbg] .text:004015D4 push eax .text:004015D5 call sub_4010A0 .text:004015DA mov esp, ebp .text:004015DC pop ebp .text:004015DD retn .text:004015DD sub_4015A0 endp
This routine loops over the null-byte terminated string in unk_404074, and XORs it with 0x81. It writes the result to the local variable olly_dbg. Here is the encrypted string in unk_404074:
.rdata:00404074 unk_404074 db 0EEh ; e ; DATA XREF: sub_4015A0+9o .rdata:00404075 db 0EDh ; f .rdata:00404076 db 0EDh ; f .rdata:00404077 db 0F8h ; ° .rdata:00404078 db 0E5h ; s .rdata:00404079 db 0E3h ; p .rdata:0040407A db 0E6h ; µ .rdata:0040407B db 0AFh ; » .rdata:0040407C db 0E4h ; S .rdata:0040407D db 0F9h ; · .rdata:0040407E db 0E4h ; S
And this is the result in olly_dbg (and the reason I named the variable olly_dbg):
debug013:0018E89C db 6Fh ; o debug013:0018E89D db 6Ch ; l debug013:0018E89E db 6Ch ; l debug013:0018E89F db 79h ; y debug013:0018E8A0 db 64h ; d debug013:0018E8A1 db 62h ; b debug013:0018E8A2 db 67h ; g debug013:0018E8A3 db 2Eh ; . debug013:0018E8A4 db 65h ; e debug013:0018E8A5 db 78h ; x debug013:0018E8A6 db 65h ; e
Next, the subroutine sub_4010A0 is called, with the ollydbg.exe string as the only argument:
.text:004015D1 lea eax, [ebp+olly_dbg] .text:004015D4 push eax .text:004015D5 call sub_4010A0
The routine sub_4010A0 retrieves the address of three exported functions from the DLL PSAPI.dll (in esi, not shown):
.text:00401230 push offset aEnumprocesses ; "EnumProcesses" .text:00401235 push esi ; hModule .text:00401236 call GetProcAddress .text:0040123C mov [ebp+enum_processes], eax .text:00401242 push offset aEnumprocessmod ; "EnumProcessModules" .text:00401247 push esi ; hModule .text:00401248 call GetProcAddress .text:0040124E mov [ebp+enum_process_modules], eax .text:00401254 push offset aGetmodulebasen ; "GetModuleBaseNameA" .text:00401259 push esi ; hModule .text:0040125A call GetProcAddress .text:00401260 mov [ebp+get_module_base_name], eax
The API EnumProcesses is called first to enumerate all running processes:
.text:0040129D call [ebp+enum_processes] .text:004012A3 test eax, eax .text:004012A5 jz loc_401488 .text:004012AB mov eax, [ebp+var_4] .text:004012AE shr eax, 2 .text:004012B1 mov [ebp+nr_processes], eax
Next, our subroutine iterates over these processes (not shown) and enumerates all modules of the current process:
.text:004012D6 mov eax, [ebp+ebx*4+dwProcessId] .text:004012DD push eax ; dwProcessId .text:004012DE push 0 ; bInheritHandle .text:004012E0 push 410h ; dwDesiredAccess .text:004012E5 call OpenProcess .text:004012EB mov edi, eax .text:004012ED test edi, edi .text:004012EF jz short loc_40131D .text:004012F1 lea eax, [ebp+var_4] .text:004012F4 push eax .text:004012F5 push 4 .text:004012F7 lea eax, [ebp+var_8] .text:004012FA push eax .text:004012FB push edi .text:004012FC call [ebp+enum_process_modules]
For each module the code then gets its basename:
.text:0040130B lea eax, [ebp+modulebasename] .text:00401311 push eax .text:00401312 mov eax, [ebp+var_8] .text:00401315 push eax .text:00401316 push edi .text:00401317 call [ebp+get_module_base_name]
It then converts the name to upper case and compares it to OLLYDBG.EXE:
.text:00401324 lea eax, [ebp+modulebasename] .text:0040132A push eax .text:0040132B call to_upper_case .text:00401330 pop ecx .text:00401331 mov ecx, eax .text:00401333 lea edx, [ebp+olly_dbg] .text:00401339 sub edx, ecx .text:0040133B .text:0040133B loc_40133B: ; CODE XREF: sub_4010A0+2A5j .text:0040133B mov al, [ecx] .text:0040133D cmp al, [ecx+edx] .text:00401340 jnz short loc_40134B .text:00401342 inc ecx .text:00401343 test al, al .text:00401345 jnz short loc_40133B .text:00401347 xor eax, eax .text:00401349 jmp short loc_401350 .text:0040134B ; --------------------------------------------------------------------------- .text:0040134B .text:0040134B loc_40134B: ; CODE XREF: sub_4010A0+2A0j .text:0040134B sbb eax, eax .text:0040134D sbb eax, 0FFFFFFFFh
If one of the base name matches ollydbg.exe (case insensitive), then eax = 0 and the code will jump to the end of the subroutine, otherwise it sets eax = -1 and continues. Or in pseudo code:
FOR ALL running processes:
FOR ALL process modules:
IF uppercase(base name of module) = "OLLYDBG.EXE" THEN
RETURN
ELSE
proceed
END IF
END FOR
END FOR
The relevant jump is “401345 jnz short loc_40133B”:

If the zero flag is set here, if means the code found an ollydbg.exe process. To patch away the check we can just change the target of the jump to loc_40134B, where we would end up if no process matches ollydbg.exe. After patching the code looks like this:

IsDebuggerPresent
Still inside sub_4010A0 we get to these lines:
.text:0040151E lea ecx, [ebp+isDebuggerPresent] .text:00401521 mov edx, offset unk_404080 .text:00401526 mov eax, [edx] .text:00401528 mov [ecx], eax .text:0040152A mov eax, [edx+4] .text:0040152D mov [ecx+4], eax .text:00401530 mov eax, [edx+8] .text:00401533 mov [ecx+8], eax .text:00401536 mov eax, [edx+0Ch] .text:00401539 mov [ecx+0Ch], eax .text:0040153C mov ax, [edx+10h] .text:00401540 mov [ecx+10h], ax .text:00401544 xor eax, eax .text:00401546 jmp short loc_40154E .text:00401548 ; --------------------------------------------------------------------------- .text:00401548 .text:00401548 loc_401548: ; CODE XREF: sub_401500+51j .text:00401548 xor [ebp+eax+isDebuggerPresent], 82h .text:0040154D inc eax .text:0040154E .text:0040154E loc_40154E: ; CODE XREF: sub_401500+46j .text:0040154E cmp eax, 12h .text:00401551 jb short loc_401548
Again they implement an XOR decryption of a string, this time in unk_404080:
.rdata:00404080 unk_404080 db 0CBh ; - ; DATA XREF: sub_401500+21o .rdata:00404081 db 0F1h ; ± .rdata:00404082 db 0C6h ; ¦ .rdata:00404083 db 0E7h ; t .rdata:00404084 db 0E0h ; a .rdata:00404085 db 0F7h ; ˜ .rdata:00404086 db 0E5h ; s .rdata:00404087 db 0E5h ; s .rdata:00404088 db 0E7h ; t .rdata:00404089 db 0F0h ; = .rdata:0040408A db 0D2h ; - .rdata:0040408B db 0F0h ; = .rdata:0040408C db 0E7h ; t .rdata:0040408D db 0F1h ; ± .rdata:0040408E db 0E7h ; t .rdata:0040408F db 0ECh ; 8 .rdata:00404090 db 0F6h ; ÷ .rdata:00404091 db 0
All characters are XORed with 0x82. The result is the string “IsDebuggerPresent”:
debug013:0018E896 db 49h ; I debug013:0018E897 db 73h ; s debug013:0018E898 db 44h ; D debug013:0018E899 db 65h ; e debug013:0018E89A db 62h ; b debug013:0018E89B db 75h ; u debug013:0018E89C db 67h ; g debug013:0018E89D db 67h ; g debug013:0018E89E db 65h ; e debug013:0018E89F db 72h ; r debug013:0018E8A0 db 50h ; P debug013:0018E8A1 db 72h ; r debug013:0018E8A2 db 65h ; e debug013:0018E8A3 db 73h ; s debug013:0018E8A4 db 65h ; e debug013:0018E8A5 db 6Eh ; n debug013:0018E8A6 db 74h ; t
An API call to GetProcAddress then gets the address IsDebuggerPresent inside kernel32.dll:
.text:00401557 lea eax, [ebp+isDebuggerPresent] .text:0040155A push eax ; lpProcName .text:0040155B push ebx ; hModule .text:0040155C call GetProcAddress .text:00401562 mov edx, eax .text:00401564 lea edi, [ebp+isDebuggerPresent] .text:00401567 xor eax, eax .text:00401569 mov ecx, 12h .text:0040156E rep stosb .text:00401570 test edx, edx .text:00401572 jz short loc_40157A
The code then makes a call to IsDebuggerPresent and tests the return value:
.text:00401574 call edx .text:00401576 test eax, eax .text:00401578 jnz short loc_40157E
If IsDebuggerPresent returns a non-zero value (meaning there is a debugger present), the code will jump to loc_40157E. To prevent this jump – even when a debugger is present – we can simply remove this jump altogether:

becomes

These two anti-debugging checks prevent that the correct code is written to 0x80000000. Now that we have removed both checks, we can finally run the code with a debugger and inspect validate_serial:
Validate Serial
Reverse Engineering validate_serial
This snippet is validate_serial when the anti-debugging checks are removed or circumvented:
debug076:08000000 push ebx debug076:08000001 mov eax, [esp+8] debug076:08000005 mov edx, 0BEEDh debug076:0800000A jmp short loc_8000020 debug076:0800000C debug076:0800000C loc_800000C: debug076:0800000C mov ecx, edx debug076:0800000E shl ecx, 5 debug076:08000011 inc ecx debug076:08000012 movzx ebx, byte ptr [eax] debug076:08000015 xor ecx, ebx debug076:08000017 mov edx, ecx debug076:08000019 xor edx, offset unk_12345678 debug076:0800001F inc eax debug076:08000020 debug076:08000020 loc_8000020: debug076:08000020 cmp byte ptr [eax], 0 debug076:08000023 jnz short loc_800000C debug076:08000025 mov eax, edx debug076:08000027 pop ebx debug076:08000028 retn
This simple routine can be represented by the following pseudo code:
FUNCTION validate_serial(serial)
v = 0xBEED
FOR c IN serial DO
v = (v*32 + 1)
v ^= c
v ^= 0x12345678
RETURN v & 0xFFFFFFFF
ENDFUNCTION
The return value of validate_serial will be compared to 0xB528B18B, if it matches, the serial is valid. So at this point we could start writing a brute-force algorithm, that tests random serials and finds the ones that are valid. Since the return value of validate_serial is only 4 bytes, or 2^32, brute forcing won’t take too long. There is a better method though.
Reformulating the Algorithm
The characters of the serial are XORed with the variable v. Due to the associative and commutative property of the XOR operation, we can separate the routine validate_serial into two parts:
FUNCTION validate_serial(serial)
q = 0xBEED
FOR i = 0 TO len(serial) - 1 DO
q = (q*32 + 1)
q ^= 0x12345678
r = 0
FOR c IN serial DO
r = r*32
r ^= c
c = (q ^ r)
RETURN c & 0xFFFFFFFF
ENDFUNCTION
The first part, calculating q, only depends on the length of the serial.
Algorithm as 32 Equations
Let qi be the ith bit of q, where q0 is the least significant bit. So q = q31q30…q0. Similarly, let c = c31c30…c0 be the return value of validate_serial, and d = d31…d0 be the desired value 0xB528B18B. Also, let si be the ith digit of the serial, and let l be the length of the serial, i.e., s = s0s1s2…sl − 1. Again, let sji denote the j bit of the digit si. The digits are encoded in ASCII, which uses 8 bits, so si = s0is1i…s7i. With this notation, we can write the bits ci as 32 equations. This is c for serials of length 2 (l = 2):
$$ \begin{aligned} c_{0} = q_{0} \oplus s^{1}{0} &\stackrel{!}{=} d{0} & c_{1} = q_{1} \oplus s^{1}{1} &\stackrel{!}{=} d{1} & c_{2} = q_{2} \oplus s^{1}{2} &\stackrel{!}{=} d{2} & c_{3} = q_{3} \oplus s^{1}{3} &\stackrel{!}{=} d{3} \ c_{4} = q_{4} \oplus s^{1}{4} &\stackrel{!}{=} d{4} & c_{5} = q_{5} \oplus s^{0}{0} \oplus s^{1}{5} &\stackrel{!}{=} d_{5} & c_{6} = q_{6} \oplus s^{0}{1} \oplus s^{1}{6} &\stackrel{!}{=} d_{6} & c_{7} = q_{7} \oplus s^{0}{2} \oplus s^{1}{7} &\stackrel{!}{=} d_{7} \ c_{8} = q_{8} \oplus s^{0}{3} &\stackrel{!}{=} d{8} & c_{9} = q_{9} \oplus s^{0}{4} &\stackrel{!}{=} d{9} & c_{10} = q_{10} \oplus s^{0}{5} &\stackrel{!}{=} d{10} & c_{11} = q_{11} \oplus s^{0}{6} &\stackrel{!}{=} d{11} \ c_{12} = q_{12} \oplus s^{0}{7} &\stackrel{!}{=} d{12} & c_{13} = q_{13} &\stackrel{!}{=} d_{13} & c_{14} = q_{14} &\stackrel{!}{=} d_{14} & c_{15} = q_{15} &\stackrel{!}{=} d_{15} \ c_{16} = q_{16} &\stackrel{!}{=} d_{16} & c_{17} = q_{17} &\stackrel{!}{=} d_{17} & c_{18} = q_{18} &\stackrel{!}{=} d_{18} & c_{19} = q_{19} &\stackrel{!}{=} d_{19} \ c_{20} = q_{20} &\stackrel{!}{=} d_{20} & c_{21} = q_{21} &\stackrel{!}{=} d_{21} & c_{22} = q_{22} &\stackrel{!}{=} d_{22} & c_{23} = q_{23} &\stackrel{!}{=} d_{23} \ c_{24} = q_{24} &\stackrel{!}{=} d_{24} & c_{25} = q_{25} &\stackrel{!}{=} d_{25} & c_{26} = q_{26} &\stackrel{!}{=} d_{26} & c_{27} = q_{27} &\stackrel{!}{=} d_{27} \ c_{28} = q_{28} &\stackrel{!}{=} d_{28} & c_{29} = q_{29} &\stackrel{!}{=} d_{29} & c_{30} = q_{30} &\stackrel{!}{=} d_{30} & c_{31} = q_{31} &\stackrel{!}{=} d_{31} \ \end{aligned} $$
We can calculate q for a given serial length l, and we know the bits di of the desired value. Also, since we need to enter the serial by keyboard, let`s force si < 128, which means s7i = 0. Using these known values and representing the indices of the serial digits si in terms of the serial length l we get:
$$ \begin{aligned} 1 \oplus s^{l-1}{0} &\stackrel{!}{=} 1, & 0 \oplus s^{l-1}{1} &\stackrel{!}{=} 1, & 0 \oplus s^{l-1}{2} &\stackrel{!}{=} 0, & 1 \oplus s^{l-1}{3} &\stackrel{!}{=} 1\ 1 \oplus s^{l-1}{4} &\stackrel{!}{=} 0, & 0 \oplus s^{l-2}{0} \oplus s^{l-1}{5} &\stackrel{!}{=} 0, & 1 \oplus s^{l-2}{1} \oplus s^{l-1}{6} &\stackrel{!}{=} 0, & 0 \oplus s^{l-2}{2} &\stackrel{!}{=} 1\ 1 \oplus s^{l-2}{3} &\stackrel{!}{=} 1, & 0 \oplus s^{l-2}{4} &\stackrel{!}{=} 0, & 1 \oplus s^{l-3}{0} \oplus s^{l-2}{5} &\stackrel{!}{=} 0, & 1 \oplus s^{l-3}{1} \oplus s^{l-2}{6} &\stackrel{!}{=} 0\ 1 \oplus s^{l-3}{2} &\stackrel{!}{=} 1, & 1 \oplus s^{l-3}{3} &\stackrel{!}{=} 1, & 1 \oplus s^{l-3}{4} &\stackrel{!}{=} 0, & 1 \oplus s^{l-4}{0} \oplus s^{l-3}{5} &\stackrel{!}{=} 1\ 1 \oplus s^{l-4}{1} \oplus s^{l-3}{6} &\stackrel{!}{=} 0, & 1 \oplus s^{l-4}{2} &\stackrel{!}{=} 0, & 0 \oplus s^{l-4}{3} &\stackrel{!}{=} 0, & 1 \oplus s^{l-4}{4} &\stackrel{!}{=} 1\ 0 \oplus s^{l-5}{0} \oplus s^{l-4}{5} &\stackrel{!}{=} 0, & 0 \oplus s^{l-5}{1} \oplus s^{l-4}{6} &\stackrel{!}{=} 1, & 1 \oplus s^{l-5}{2} &\stackrel{!}{=} 0, & 0 \oplus s^{l-5}{3} &\stackrel{!}{=} 0\ 1 \oplus s^{l-5}{4} &\stackrel{!}{=} 1, & 1 \oplus s^{l-6}{0} \oplus s^{l-5}{5} &\stackrel{!}{=} 0, & 0 \oplus s^{l-6}{1} \oplus s^{l-5}{6} &\stackrel{!}{=} 1, & 1 \oplus s^{l-6}{2} &\stackrel{!}{=} 0\ 1 \oplus s^{l-6}{3} &\stackrel{!}{=} 1, & 1 \oplus s^{l-6}{4} &\stackrel{!}{=} 1, & 1 \oplus s^{l-7}{0} \oplus s^{l-6}{5} &\stackrel{!}{=} 0, & 0 \oplus s^{l-7}{1} \oplus s^{l-6}{6} &\stackrel{!}{=} 1\ \end{aligned} $$
Solving the equations
If l < 7, then all terms syl − x with l − x < 0 disappear. This means, that in order to fulfill the last equation:
$$ 0 \oplus s^{l-7}{1} \oplus s^{l-6}{6} \stackrel{!}{=} 1 $$
the length l must be 6 or larger, otherwise we would get $0 \stackrel{!}{=} 1$ . Solving the equations is easy, because each bit of the serial affects at most one equation. Some bits have no influence at all, for instance only the last seven digits of the serial influence validate_serial. For other bits of the serial we have equations that tell us its definite value, e.g., $1 \oplus s^{l-3}_{2} \stackrel{!}{=} 1$ means s2l − 3 = 0. A third kind of bits appear together with a second bit from the serial, here we have two choice to set the bits. For example:
$$ 1 \oplus s^{l-4}{1} \oplus s^{l-3}{6} \stackrel{!}{=} 0, $$
means that either s1l − 4 = 0, s6l − 3 = 1 or s1l − 4 = 1, s6l − 3 = 0.
Keygen
Our keygen has one additional requirement: the serial needs to be enter by keyboard. It should therefore contain only printable ASCII character – the following keygen requires the serial to have only alphanumeric characters. My keygen performs the following steps:
- First, randomly determine a serial length l greater or equal 6.
- Next, initialize all digits of the serial with random, alphanumeric characters.
- Next, change the bits of the serial to fulfill the equations, thereby randomly choosing whenever there are two choices.
- Check if the resulting serial is alphanumeric, if not, repeat step 2.
It takes about 30 trials on average to get a valid serial this way. The following is an implementation of the keygen algorithm in Python:
import random
def digit_to_ascii(digit):
s = 0
for i in range(8):
s += digit[i]*(1 << i)
return chr(s)
def key_from_digits(digits):
key = ""
for d in digits:
key += digit_to_ascii(d)
return key
def calc_q(l):
q = 0xBEED
for i in range(l):
q = (q*32 + 1)
q ^= 0x12345678
q = q & 0xFFFFFFFF
return q
def get_equations(l):
terms = [[] for i in range(32)]
even_odd = 32*[0]
for i in range(32):
terms[i] = []
for i in range(l):
""" do the shl by 5 bl """
terms = [[] for i in range(5)] + terms[:-5]
for j in range(8):
""" the last bit of digl must be zero for ASCII """
if j < 7:
terms[j].append((i,j))
""" q is the constant term """
q = calc_q(l)
for i in range(32):
even_odd[i] ^= ((q & (1 << i) ) >> i)
wanted = 0x0B528B18B
for i in range(32):
even_odd[i] ^= ((wanted & (1 << i) ) >> i)
return terms, even_odd
def generate_key_with_given_length(l):
terms, even_odd = get_equations(l)
while True:
digits = [8*[0] for i in range(l)]
for d in digits:
while True:
for p in range(7):
d[p] = random.randint(0,1)
if digit_to_ascii(d).isalnum():
break
for t, eo in zip(terms, even_odd):
""" we can randomly pick all but one term """
s = 0
for i in range(len(t)-1):
digit, place = t[i]
digits[digit][place] = random.randint(0,1)
s += digits[digit][place]
digit, place = t[-1]
digits[digit][place] = eo ^ s
""" only return alpha numeric keys, try again if key isn't """
key = key_from_digits(digits)
if key.isalnum():
return key
def generate_key_with_random_length():
""" any length greater than 5 should do """
l = random.randint(6,20)
return generate_key_with_given_length(l)
for i in range(100):
print(generate_key_with_random_length())
The code generates 100 valid serials:
$ python3 keygen.py Uw4ddG1G2 GdXfstRnP1EDG0dR jkxxddEpdR GLSQNlL4flHeEepg2 NMtRyVHp0AL4ddEqDR eDEpg2 eEdPdR VGDbPqL8icWqOteEdPdR 6tnFDqiDdDQG2 Qlxb4nG9kz5EEdPdR hJyDedPdR ...
Entering one of those serials leads to the good boy message: